Pythagorea Medians And Mid-Points Level 4.11 Solution/Answer

Pythagorea Medians And Mid-Points Level 4.11 New Version Game Answers, detailed solutions, Tips, and Walkthrough. Scroll below to find answer to this level.
Pythagorea is android/iOS app developed by Horis International Limited. Solutions hints and answers to pythagorea are available in this post scroll down to find solutions to all the levels.
This game is mostly focused on geometric puzzles and construction. The workspace is divided into grids to draw lines. You should know all the basic Math operations. All lines and shapes are drawn on a grid whose cells are squares. Most of the game levels can be answered using natural intuition and by some basic laws of geometry.
Click Here for All other Pythagorea Levels: http://puzzlegamemaster.com/pythagorea/

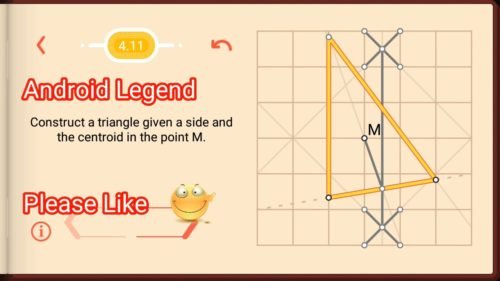
Pythagorea Level 4.11: Construct a triangle given a side and the centroid in the point M.
If you have any doubt regarding Pythagorea answers given here you can watch video below or you can comment on this post-
I will answer the questions about how to extend 50%, as suggested. In the (I) info section it tells you that a centroid cuts the medians that run thru it into 1/3 & 2/3 lengths, the longer side between the vertices and the centroid. As someone suggested, you can simply draw line segments from each vertex to the centroid M. That will leave faint lines extending off the grid. Since M and vertices are all on nodes, it’s easy to see that the new lines cross two vertical grid lines from the right vertex and one from the left. Therefore to extend them go one vertical grid line further from the left to obtain half the distance from vertex to M and mark that point. To extend the line from the left vertex a half vertical grid line further you will need to make little crisscrosses in a “cell” between the four nodes to get a midpoint up high and another down low like the video solution on this site does for a different purpose. Mark the midpoints of those crisscrosses and connect with a line segment. Now Mark the intersection of the extension of the line from left vertex to M and the 1/2 grid line just created. Mark that point. Now you have marked what are the midpoints of the two sides that will extend up from each given vertex. The faint lines extend upwards meet at a point. Mark that point as the third vertex and complete the triangle. The sites video solution really uses the app to confirm that a line extended from the midpoint of the given side thru M intersects with a grid line above, so you can sort of guess that’s the point and try it and see it confirmed. This method specified here works without the app confirmation.
Thanks Seattle Dave, that makes sense. You helped me. Regards!
You don’t even need the middle point of the given side. You only need to know that M divides any of the medians at a ratio of 2:1. So, draw two medians from the line ends towards M and extend them by 50 percent (use the grid lines) to get a second point of each of the other sides.
How do you “extend a line by 50 percent”??
Nevermind, got it. Thx.
I don’t. how do you know how long 50% is? or as Steve Warren is asking: how do you know the angle of the second side?
I was only interested in the last solution and after watching it, I am convinced that it makes absolutely zero mathematical sense. How did you know to draw these two pairs of diagonals and where to draw them?
The given line is 3 boxes long. The center of that is the middle of the center box. The diagonals were used to find the middle of that box.
I get how you get the midpoint of the given side and extend that ray from the midpoint through the centroid, but how did you know what angle to use for the second side?
good question. I love to know the answer. anyone?
How is the middle point of the given line exactly in the middle of node 2 (from the left) and node 5? If you draw the perpendicular from that point, it does not mirror the line on itself. Or am i wrong?
Got it, I was wrong :p
These solutions do not make any sense. Where can we go to see the steps of what is going on??